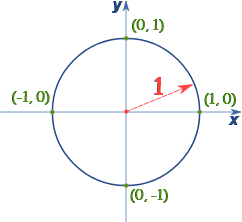
When plotting the coordinates of Sin and Cos, they will create a circle due as long as each point (cos θ, sin θ) lies on a circle of radius 1 centred at the origin.
This circle is called the unit circle.
The benefit of this is that allows Sin, Cos and Tan to be read directly as their X and Y coordinates
Calculation
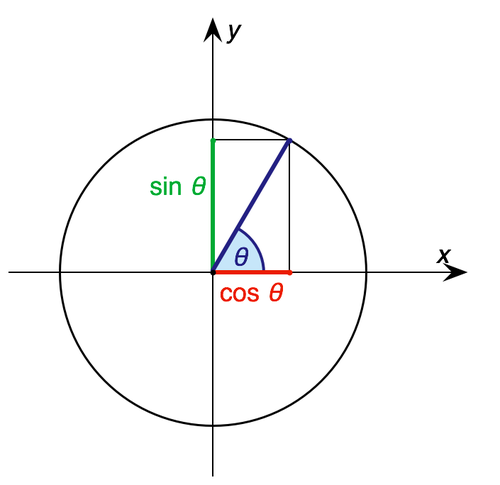
- Sin is used to calculate Y.
- Cos is used to calculate X.
Demonstration
Quadrants
Just like any other circle, the unit circle can be divided into four quadrants:
Top Left (II): -,- (180° → 90°)
Top Right (I): +,- (90° → 0°)
Bottom Left (III): -,+ (270° → 180°)
Bottom Right (IV): +,+ (0° → 270°)
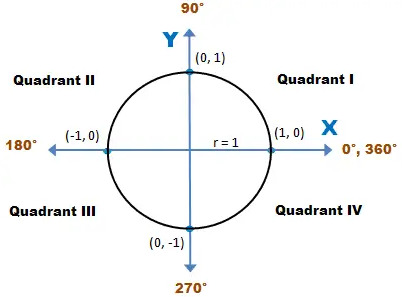
but this also has an impact on the results of Sin, Cos and Tan:
I: All are positive
II: Cosine and tangent are negative
III: Sine and cosine are negative
IV: Sine and tangent are negative
Info
This is easier to remember by considering what function(s) are positive.
A common and easy to remember method is by going anti-clockwise: All, Sine, Tangent, Cosine (ASTC).
Acronyms for this exist, such as: All Students Take Calculus
Info
Follows Cartesian Coordinates